从出土简牍文献看中国早期的正负数概念 ,对于想了解历史故事的朋友们来说，从出土简牍文献看中国早期的正负数概念是一个非常想了解的问题，下面小编就带领大家看看这个问题。

原文标题：从出土简牍文献看中国早期的正负数概念

（中国科学院自然科学史研究所）
摘要 将出土文献和传世文献中某些涉及政府考评工作的材料结合起来进行深入的分析，可以廓清一些关于中国古代正负数概念的认识误区，幷建立正负数概念的早期历史。本文提出判断古人使用正负数概念的标準是对立相反的性质被嵌入到数量中成爲数量本身的一部分；考辨了《算数书》“医”条中“算”字不可能是一些学者所认爲的赋税单位或一般意义的钱的单位，“医”条既非讲医生治病时的收入与交税，也非讲收入与成本。本文论证“医”条规定了合格医生治病时成功与失败的最低比例，而“算”字则是考核医生治病效果的计分单位。利用语法分析的方法，本文证明“医”条和董仲舒《考功名》确实应用了正负数概念，而居延和敦煌汉简的一些疑似例证是否用到正负数概念，则因信息不充分而不能判定。作者认爲得失、成败等相反的观念虽是正负数概念産生的基础，但先秦时期方程算法的特殊结构才是推动正负数概念産生的决定力量，新兴的正负数概念影响到政府的考核和评价方法，“医”条和《考功名》（不排除居延汉简等中的某些条目）体现了这种影响。本文还分析了这种考评方法中使用正负数概念的特点。文章最后就研究的方法进行了初步的探讨，特别强调了语法分析方法和知识结构观念的重要性。
关键词：正负数概念，《算数书》“医”条，《九章算术》方程算法，《春秋繁露·考功名》，出土简牍文献，上古数学史，上古官方考评法，语法和知识结构分析法
目次
一 引言
二 用对立相反的意义刻画数量的性质是正负数概念的核心
三 《算数书》“医”条不会是针对税收的问题
四 收入成本说在证据上太孤立
五 正、负数观念用于考核
六 正、负数概念是先秦方程算法的特殊结构之必然産物
七 早期正负数概念与考核评价记录
八 余论——关于方法论的初步讨论
一 引 言
负数的引入是数学史上数量观念的重要变革。学术界曾长期认爲，负数概念的使用以中国古代数学经典《九章算术》的方程章爲最早。该章用“正”、“负”两个术语来描述数量的性质，不仅有描述正数、负数加减法则的“正负术”，而且在实际运算中用到正、负数的乘除法，从而确立了中国在世界上最早使用负数的优先地位，也确立了负数出现的时间下限爲《九章算术》的编成时代——现在一般定在公元前一世纪中叶。但是，下限幷不意味着最早使用负数的时间。如李俨先生推测负数的産生不晚于秦代，但他没有提供具体的证据[1]。郭世荣先生认爲负数概念的出现要比《九章算术》的记载早一些。他搜集了西北出土汉简中的一些用例，认爲其中用到正负数的加减法，反映了从出现负数概念到确立正负数运算法则过程中的中间环节。他还从打分的角度解释了个别条目[2]。于振波先生也研究了汉简中一批关于“得若干算”、“负若干算”的用例，肯定了永田英正早年关于它们是考评记分用语的判断[3]，认爲“得算”与“负算”和《九章算术》的正数与负数观念相近[4]。邹大海曾参考郭、于二先生的研究，再与睡虎地秦简、郑衆对《周礼》“九数”的注释、刘徽对《九章算术》编纂历史的记录等文献结合，推论负数概念産生的思维背景虽是现实生活中存在的欠、不足、罚等观念，而其正式産生则是源于战国时代方程运算中出现被减数不足减的情形[5]。
2000年9月公布的湖北江陵张家山西汉初年墓（墓主约于公元前186年去世）内出土的《算数书》中有一个题名爲“医”的条目，爲讨论早期的正负数概念提供了新的材料。邹大海认爲“医”条中“得若干算’和‘负若干算’应是一种考课记分”。它“把先秦数学中已有的负数概念用于对医生治病效果的考核”[6]。郭书春[7]、王青建、张新立[8]先生也同意“医”条中有负数概念的使用。
古克礼（Christopher Cullen）先生[9]则认爲“医”条中的“负”是欠的意思，“算”字被译爲“string of cash”（钱串）。他没提及“负若干算”是否含负数概念，但显然他不认同这一点。林仓亿先生[10]称 “指出”“两种可能解读方向”，一种是“算”字表示赋税单位，“医”条是讲医生的缴税问题，这与古克礼先生的意见相似。另一种是“算”爲考核的单位，“医”条是讲对医生的考核。林先生倾向于后者，这与邹大海提出的意见相同，但他否认“负若干算”用到负数概念，且没有说明理由。另外还有一些学者持林先生所说的前一种意见[11]。
日本张家山汉简“算数书”研究会则认爲“医”条的“得若干算”、“负若干算”分别是医生的收入和用于药物与治疗的支出。他们没有涉及其中是否含有负数概念的使用问题[12]。
上述研究大都较爲零散，论证还不够充分，考虑也不太全面，因此见仁见识。本文利用出土文献和传世文献相结合，从微观和宏观两个方面，对我国正负数概念的早期发展做一较爲系统和深入的研究。
由于数学概念从産生到定义有时是一个历史的过程，因此首先需要明确古人具有某个数学概念的标识是什麽。所以，本文首先要确立判定正负数概念産生的标準。由于《算数书》比现存汉编《九章》至少早一个多世纪，因此对它是否含有正、负数概念的认定就显得很重要。所以，本文要重点考察“医”条的“算”究是何意，幷判断该条是否含有正负数概念的应用。然后，本文要结合其他文献对上古时代的正负数概念在政府管理中的考评方法上的应用做一考察，幷推断正负数概念的産生时代，刻画其内涵和特点在考评中的体现。最后，本文还要简要讨论一下方法论的问题，特别强调语法分析的方法和知识结构的概念在考察科学概念和科学思想时的重要性。
二 用对立相反的意义刻画数量的性质是正负数概念的核心
李俨先生说：“自然数産生后，必然要运算，运算离不了加减乘除，减不了便産生负数，除不尽便産生分数、正整数。分数、负数构成了有理数系。在中国周、秦间已具备了这个数系的雏型，其发展程序大概是先有正整数的运算，其次産生了分数，在后期産生了负数。”[13]这很好地描述了数概念发展的逻辑。
在古代，数学概念的産生与使用幷不经常以明确的定义爲前提，不仅在开始使用自然数的时代，甚至在已广泛使用分数的很长时间内，人们都幷没有对它们进行适当的定义或大致的界定。正负数概念的使用也是如此。正、负是两个相互对立和彼此依存的概念，没有负的观念也就没有与之相反的正的观念。负数概念与正数概念的关係也是如此。它们是同时産生的。当对立相反的意义被用于刻画数量的性质幷成爲数量本身的一部分时，就産生了新的负数概念，原来认识的数就成了正数。
中国最早给出正、负数界定的是三世纪的刘徽，他认爲如果有两个数量的意义“得失相反”，就需要用正、负来刻画它们（引文及分析详后）。但他前后的学者大多不刻意去定义正、负数的内涵，数学家对正、负数内涵的揭示也处于一个发展变化的过程中。负数现在被视爲比零还小，与正数相反的数。但从历史的发展来看，正、负相反的概念被用于刻画数的性质是産生正、负数概念的关键步骤，这在时间上远早于刘徽。在《九章算术》方程章中用到正、负数的问题的作者，其心中虽有某种形式的“零”的观念，但他们幷没有把“没有什麽东西”这类观念视爲一个数“零”的明确意图，刘徽对正、负数的界定也不涉及零。因此，我们认爲正、负数概念的産生应以正、负相反的意义被用于数量性质的刻画幷成爲数量本身的不可分割部分爲标识，而比零还小的数这种观念应视爲人类在认识负数的历史中的重大进展。下面的讨论以此爲基本标準来展开。我们先来看《算数书》“医”条的情况。
三 《算数书》“医”条不会是针对税收的问题
“医”条在《张家山汉墓竹简[二四七号墓]》中的释文如下：
医 程曰：医治病者得六十筭□□廿筭□□程□弗
从出土简牍文献看中国早期的正负数概念得六十而负几何？曰：负十七筭二百六十九分筭十一。其术曰：以今得筭爲法，令六十乘负筭爲实。[14]
这一条含有第72、73号两支简，从“得六十”起属于第73号。何有祖把“□□廿筭□□程□”释读爲“而负廿筭有□程及弗”[15]，爲林仓亿[16]采用（林所引爲何有祖2004年12月26日刊于简帛研究网的文章“张家山汉简释文与注释商补”，见http://www.jianbo.org/admin3/html/heyouzhu07. htm）。而整理小组后来的版本则只补释了“廿”前的“负”字[17]。把前两个“□”释读爲“而负”，这与照片上残存笔划和上下文都吻合，应该没有问题；而且“得六十筭而负廿筭”与第73号简中开头的“得六十而负几何”句式结构相同。第72号简文字漫灭甚多，释文中“
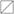
从出土简牍文献看中国早期的正负数概念”所表示的缺字占了竹简的一半，估计字数在20—30之间。由于有那麽多文字不能释读，因而把两支简连在一起读时，其具体细节仍有很多不清楚的地方。古克礼先生甚至怀疑整理者的编连是否合适，但他仍按整理者的意见把它们联在一起[18]。
从两支简的出土位置来看，虽然不是紧挨着，但也隔得很近，而且“得若干算”、“负若干算”这种用法只见于这两支简，而“得六十（算）”都见于两支简，所以它们确应如整理小组的意见，是连在一起表示同一个问题的。
(一)“医”条的“算”不会是税钱的单位
“算”和“筭”本是两字。《说文解字》“竹”部云“算，数也。从竹、具”，“筭，长六寸，计历数者。从竹、弄，言常弄乃不误也”[19]。段玉裁注“算”字条说：“筭……谓筭筹，与算数字各用，计之所谓算也，古书多不别”，注“算”字条说“筭爲算之器，算爲筭之用，二字音同而义别”[20]。这是区别“算”、“筭”二字的初始义，又指出了后来实际混用的情况。从出土的战国、秦、汉简牍文字看，当时二字确实已经混用了。《现代汉语词典》把两字都作爲字头，但只对“算”字分义项进行解释，而把“筭”作爲书面用字，说它“同‘算’”[21]。在一般的研究文献中，在不必区别二字的情况下，多按习惯作通行字处理，把“筭”字写成“算”。除引用原文外，本文一般也把“筭”写成通行字“算”。
“算（筭）”字的义项很多，不同字典、词典有不同的归类。以下据一些常见字典、词典，列出可能与“医”条有关的几个义项：（1）古代计算或记数用的工具算筹，（2）数目、数字，（3）计算，（4）计算在某个类别或数量之内，（5）政府向成年人征人头税的钱数单位，1个成年人所应交纳的人头税爲1算[22]。一算的具体钱数秦汉时代有所变化，但好多时候以120钱爲一算[23]。（6）徵税。
第（3）、（4）和（6）项爲动词，而“算”在“医”条中是名词或量词，所以它们显然不符合“医”条的语境。下面先只考虑第（1）、（2）和（5）项。
首先看“医”条的“算”是否爲第5项意思。不管“医”条具体是什麽意思，也不管“算”字何指，在“程曰：医治病者得六十筭而负廿筭”一句中，通过“而”字连接的“得六十算”和“负廿算”都以“医治病者”爲主语。因此这句的意义在很多方面都是较爲明确的：首先，“程”是计量标準，此条是政府针对治病医生在某方面的标準，以及与该标準相关的某些数量。其次是在该标準中，医生一方面是“得若干算”，另一方面是“负若干算”，“得”和“负”是相反的两种情况（但主语都是同一个“医治病者”）。在这个标準中，“得”的数量（60算）爲“负”的数量（20算）的3倍。如果算在“医”条中是政府向成年劳动力（不幼不老）徵收人头税的单位，那麽医者只能是纳税者而不可能是收税者，所以他不可能反过来还“得六十算”。退一步说，即使“得六十算”是指政府向他收取60算[24]，那麽“负廿算”就是政府给他20算的税，这样既麻烦又矛盾，何不一开始就让他只交40算的税呢？况且，一个普通劳动力一年要交的成年劳动力人头税（他还要交另一份不论年龄大小都要交的人头税“口钱”）爲一算，很难想像一个医生却要交60倍（抑或至少是20倍）的成年劳动力人头税[25]。
(二)“算”的涵义不能说明“医”系针对收缴税的说法
古克礼博士把医条的“算”字翻译成string of cash (钱串)。林仓亿先生则据“算”有人口税之义将“程曰：医治病者得六十筭而负廿筭”“解读爲医治病者的规定负税比率爲60比20”。 因爲医生不是徵税官员，所以“得60算”不可能是收取60算的税。因此，林的这种解释，实际幷不是把“算”作爲赋税的单位，而是作爲钱的单位。这样一来，林对“医”条、“算”字的理解与古克礼是很接近的。不难看出，“算”有赋税的单位这个义项幷不能爲人们把“医”条解释爲讲收税的比例这种意见提供支持：既然“医”条的“算”是钱的单位，而不是赋税的单位，那麽要把“医”条解释爲讲收缴税就不能由“算”字有赋税的单位之义来说明，而必须另有证据。可是，除此之外就没有其他证据说明“医”条是讲医生纳税的比例了。可见，认爲“医”条是针对医生收税的说法，幷没有根据。
不过，虽然把“算”字本身解释爲普通意义下的钱的单位而不是税的单位，幷不能说明“医”条乃针对医生收税的问题，但这也不能说明“医”条就一定不能解释爲针对医生收税的问题。所以，如果“算”字可以解释爲普通意义下的钱的单位的话，那麽林仓亿的上述说法也还是一种选择，因爲得到了60算的钱，又“负”20算的钱，很容易让人想到是收入60算的钱，又向政府部门交纳其中的20算。但是，把“算”理解爲普通意义下的钱的单位，却是有困难的。虽然“算”在汉代关于财産税的“訾算”中被用于指一万钱，但这种用法应该是由它表示“税”的情形转化而来的，而且只限于特定的情况。下面对此做一些分析。
文献中“算（筭）”指一万钱的，以《汉书·景帝纪》载景帝后元二年（公元前142年）五月诏及其顔师古注释所引服虔和应劭的意见爲代表。该诏书曰：
“人不患其不知，患其爲诈也；不患其不勇，患其爲暴也；不患其不富，患其亡厌也。其唯廉士，寡欲易足。今訾算十以上乃得宦，廉士算不必衆。有市籍不得宦，无訾又不得宦，朕甚湣之。訾算四得宦，亡令廉士久失职，贪夫长利。”
顔师古引服虔曰：“訾万钱，算百二十七也。”引应劭曰：“古者疾吏之贪，衣食足知荣辱，限訾十算乃得爲吏。十算，十万也。贾人有财不得爲吏，廉士无訾又不得宦，故减訾四算得宦矣。”顔师古曰：“‘訾’读与‘资’同。他皆类此。”[26]
据顔师古注，“訾”是财産。服虔的注中“算”指税或徵税，他的意思是财産1万钱，需要交纳的财産税爲127钱。而在应劭的注中，“算”虽然可以理解爲表示万钱的钱数单位，但这种理解实际来源于需要交税1算所对应的訾：“訾十算”实际是“财産达到要交十算财産税的量”或者说“需要交十算财産税的财産”，“訾四算”即“财産达到要交四算财産税的量”或者说“需要交四算财産税的财産”。财産税与财産成正比例关係，因而财産税的单位也就对应于一定数量的财産，故进而可以作爲表示财産多少的单位。《汉书》正文所载景帝的诏书和应劭的注，都说明以前对步入士途的常规限制——财産量要达到（需交）十算（财産税）的额度的人家才可以做官员，这个标準门槛太高，限制了廉士的入宦，所以要降低到财産量（需交财産税）四算的标準。这个例证实在不可以作爲“算”爲普通意义下的钱数单位的证据。既然“算”用于表示钱数的单位时总是指税钱的单位或代指财産税单位所对应的财産的单位，那麽把“算”作如是解时，“医治病者得六十筭而负廿筭”就是一句不通的话（参考上小节）。这正好说明“算”在“医”条中不应指税或钱数的单位。
另外，林把“负某算”理解爲交多少算的税也没有例证。在《后汉书》卷六十一“左雄传”记录左雄上疏：“乡部亲民之吏，皆用儒生清白任从政者，宽其负筭，增其秩禄，吏职满岁，宰府州郡乃得辟举”[27]，这裏的“负”是亏欠的意思（李贤注：“负，欠也。算，口钱也。”“负”作欠解，亦见于居延新简：“时市谷决石四千，以钦作贾，谷十三石八斗五升直觻，得钱五万五千四。凡爲钱八万，用偿所负钱”[28]），“负算”是负欠的成年劳动力人头税，没有例证表明“负”有缴纳之义（林先生把“负”解释爲背负，亦即负担，虽不合古训，也是通的。但这与交纳的区别是明显的）[29]。退言之，如果“医”条的“算”如“訾算”史事中指一万钱（这是目前所能找到的“算”不直接指税的单位而可以用于指钱数的唯一证据），那麽，即使“得六十筭而负廿筭”可以从按比例交税的角度解释爲收入60万钱而交税20万钱，这对于一个医生来说，其数额之大也是令人难以置信的。下面我们通过具体的计算来证明这一点。
与《算数书》同出于张家山247号汉墓的《二年律令》中有一处提到医生：“太医、祝长及它都官长，黄（广）乡长，万年邑长，长安厨长，秩各三百石，有丞、尉者二百石，乡部百六十石”[30]。汉初秩三百石官员的常俸，没有特别準确的记录，但可以据相关材料进行多种推算：
（1）同出一墓的《算数书》中“米出钱”条涉及粝、稗、黍的价格[31]。据推算，一处粝、稗的价格分别是每斗
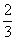
从出土简牍文献看中国早期的正负数概念钱、
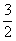
从出土简牍文献看中国早期的正负数概念钱；一处米（即粝米）、黍的价格分别爲每斗1
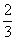
从出土简牍文献看中国早期的正负数概念钱、
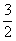
从出土简牍文献看中国早期的正负数概念钱。从后一处粝米的价格远高于前一处，可知后一处黍的价格也会比前一处的黍价要高出不少。即使按高的黍价每斗
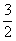
从出土简牍文献看中国早期的正负数概念钱即每石爲25钱[32]计算，如以三百石官员一年的常俸爲300石粟（黍爲粟的一种，价格应差不多），那麽折合成钱爲7500钱。
（2）据《汉书·百官公卿表》顔师古注，秩三百石官员的常俸爲每月40斛[33]，一年480斛。按《算数书》的最高标準每斗
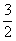
从出土简牍文献看中国早期的正负数概念钱，即每斛（容积10斗）15钱计算，那麽太医一年的常俸爲7200钱。这与第一种算法的结果非常接近。
（3）一些学者认爲，西汉常规时期的粟价在每斛30至80钱之间[34]，按最贵的粟价计算，一年常俸按300石计算，最多（按大石，即
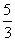
从出土简牍文献看中国早期的正负数概念斛计）折爲40000钱（如按小石即1斛计，只折爲24000钱）。
（4）如果价格仍按第3种以高限每斛80钱，一年常俸按第2种480斛计算，折合成钱最多爲38400钱。这与第3种相近而稍少。
（5）有学者怀疑顔师古注可能是把东汉禄秩等级与实际俸禄的对应关係误认爲了西汉的情况，主张从《史记》、《汉书》等书的古注和汉简中找到的一些零星资料来推算。其中没有三百石的记录，但有比六百石的月俸记录爲3000钱[35]，三百石官员的俸禄无论如何也会明显低于这个标準，因此每年常俸肯定少于36000钱。
这5种推算法中，可能性最大的第1种的数值爲7500钱。秩三百石的下级官员的其他收入很少[36]，我们多算一些，假设其他收入爲常俸的1/3，那麽总收入最多不超过10000钱，此数只有60万收入的1/60、40万税后收入的1/40，甚至只有20万税的1/20。即使按收入最高的第3种算法，太医的合法年收入也会低于（40000×1
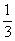
从出土简牍文献看中国早期的正负数概念=）53333
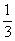
从出土简牍文献看中国早期的正负数概念钱，此数也不到总收入的1/11、税后收入的1/7，甚至只有税额的1/4稍多一点。汉代有的小县县长的禄秩也就三百石。一个普通医生[37]的收入要比三百石太医正常收入的最大极限还高出那麽倍，是不能想像的。
需要说明的是，算作爲计算税钱的单位，当然指一定数量的钱数，但这幷不意味着算是一般意义的钱的单位。高敏先生研究汉代的口钱、算赋时说“算”“是一个固定的计量单位”，幷认爲“按成年人丁徵收”的税，“其税率恰爲每人每年一算，因此就获得了算赋之名”，而一算的钱数也有变化，汉文、景帝时期爲227钱，后来减少，在某一时间变爲120钱[38]。显然，高先生“固定的计量单位”的说法，是一句解释性的话，幷非说算是一般意义上的计量单位或钱数单位，而从他文中所引述的例证看，“算”都指税收而言。另外，笔者要强调的是：没有任何证据表明算先是一个数量固定的钱数单位，然后才因爲一算的钱正好与一个成年劳动力应交的人头税相同，就把成年劳动力人头税称爲“算”。相反，算一直被用作成年劳动力人头税的单位，而其数值在不同时期有所变化，这正好说明算首先是成年劳动力人头税的单位，幷一直沿用；而随着时代和情况的变化，其具体的钱数则有所调整。笔者认爲：古代用算（即算筹，不一定是大量用于布算来进行複杂计算的那种纤细的算筹）来表示数字，有时每计一物或一事，即用算一支（参考后文）。由于年龄不太老的成年人是国家的主要劳动力，自然在经济工作中是一个很重要的统计对象，用一支算筹表示一个成年劳动力，就是很自然的事，因而在计算其人头税时，也用算爲单位。时代不同，情况有异，成人劳动力人头税虽然一直沿用算作爲一个基本的单位，但其钱数则有所调整，所以每算的钱数发生变化，自是情理之中的事。
(三)《汉书·食货志》中向医生等收税的记录不能支持认爲“医”条系针对医生收税的观点
林先生文中引《汉书·食货志》说：“工匠、医、巫、卜、祝及它方技、商贩、贾人，坐肆列里区谒舍，皆各自占所爲于其在所之县官，除其本，计其利，十一分之，而以其一爲贡。”[39]作爲“医”条系针对医生收税的证据。这是没有说服力的。
在《食货志》中，这段文字的语境是王莽时仿《周官》（即《周礼》）制度制定收税政策，上引文字只是其中一部分。这一具体的收税方法幷不见于《周礼》，王莽篡位比《算数书》的成书下限晚了近200年，王莽的整个作法又不属于常规的情况，所以用这段文字来说明“医”条的情况，本来就没有多大的说服力。而且就算它能反映“医”条时代针对医生收税的情况，则我们也不难发现这正好说明“医”条反而不会是针对医生收税的问题。因爲这段文字说工匠、医生、巫师、商人等在经营时，都要自己估算其收支、利润，报给所在县的官府，从收入中除去本钱，将余下利润的11分之1交税（“贡”）。如果“医”条讲的也是收税，那麽即使“医”条的“得若干算”的也是利润（其实如果这条一定要解释爲按比例交税，那麽“得若干算”应该解释爲收入“若干算”，林文也解释爲收入而不是利润），则“医”条的税率（3分之1）是《食货志》所说的“贡”率的3
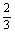
从出土简牍文献看中国早期的正负数概念倍，接近4倍。而把“得若干算”按正常情况解释爲收入时，利润就会比60算低不少，这时“医”条的税率就比3分之1要高出不少，因而比“食货志”的“贡”率还要高得更多。可见，即使“算”不一定指万钱，而可以是别的小数目，“医”条和“食货志”中的两个税率所存在的巨大差距，也说明把“医”条按税率解释是完全不妥当的。
顺便说一下，与《算数书》同出于张家山247号汉墓的《二年律令》也出现“算”、“得”和“负”。其中“算”指收税，“负”指赔偿（也有一处表示装载货物），但没有“负算”或“负若干算”、“得算”或“得若干算”的例证，“得”和“负”二字没有同时用来与同一事物发生联繫。律令中只有一处有“医”字，提到太医的俸禄爲三百石（详上节注释），但与“得”、“负”、“算”都不发生关係，也未提到向医生收税的事情。所以这对于用收税来解释“医”条的观点不能提供丝毫的支持。
总之，“医”条的“算”不能理解爲“赋税”或钱的单位。把“医”条解释爲针对医生收税的问题不仅没有证据，而且会出现矛盾。
四 收入成本说在证据上太孤立
日本张家山汉简“算数书”研究会认爲“得若干算”和“负若干算”分别是医生治病时得到的报酬和医生用于治疗的花费。这实际也是把“算”字作爲钱的计量单位来看待。这种解释比上述用收税来作的解释要合理一些，因爲它不会导致“医”条文本内部的矛盾。不过，这种意见缺乏证据。不仅“医”条本身对此没有任何的明示或暗示，而且也没有其他的材料表明当时的政府部门对医生的收入与成本的比例制定了标準。事实上，由于难以预料社会上疾病在不同时期的发生情况和医药材料市场的变化，要规定这种收支的比例是不现实的，而且也没有必要。该研究会也提到永田英正关于居延汉简中“得算”、“负算”用于考核记分的意见，不知爲何不把二者统一起来，反而要提出一个证据上更孤立的解释。
下面从多个方面对有关问题进行细緻的梳理和论证。其中，用语法分析的方法对古代文献的作者是否具有正负数的观念这一问题进行解析，是很关键的。
五 正、负数观念用于考核
（一）“算”表示数量，用于记数
下面我们看第（1）、（2）两个义项,它们有密切关係的。作爲计算和记数用的工具算筹，算表示的就是数量。远古的时候，人们用结绳、刻木、小石头等实物，通过一一对应来记录物品数量，长条形的小竹（或木）棍也是其中之一。后来有些从事与计算相关的专门工作的人出于方便，把这种用于记数的长条形物品逐渐赋予一定的形制和规格，再逐渐加上一套规则，便成爲“算（筭）”即算筹（又有筹、策等名称）。记数和计算的算筹，还可能在不同的使用场合有不同的形制与功用[40]。因此，“算”一方面表示算筹，另一方面也表示数量。“算”用来表示数量，在古代用得很多：如《仪礼·乡射礼》、《礼记·投壶》、《大戴礼记·投壶》中，用一尺二寸长的木片（亦称爲“算”，但与专门用于较複杂计算的细长算筹在形制上有所不同）来记数。其中《礼记·投壶》说：
“投壶之礼：主人奉矢，司射奉中，使人执壶。主人请曰：‘某有枉矢、哨壶，请以乐宾。’……司射进度壶，间以二矢半，反位，设中，东面，执八算兴。……有入者，则司射坐而释一算焉。宾党于右，主党于左。卒投，司射执算曰：‘左右卒投，请数。’二算爲纯，一纯以取，一算爲奇。遂以奇算告，曰：‘某贤于某若干纯。’奇则曰‘奇’，钧则曰‘左右钧’。命酌，曰：‘请行觞。’酌者曰：‘诺。’当饮者皆跪，奉觞曰：‘赐灌。’胜者跪曰：‘敬养。’正爵既行，请立马，马各直其算。一马从二马，以庆。庆礼曰：‘三马既备，请庆多马。’宾主皆曰：‘诺。’正爵既行，请彻马。算多少视其坐。筹，室中五扶，堂上七扶，庭中九扶。算长尺二寸。”[41]
主人请客人玩一种叫投壶的游戏，它有一定的礼仪：先是主人、司射和另一个人分别拿着要投的矢（箭）、中、壶等器具，然后主人和客人进行一些礼节性的请让，客人接受投矢之请。通过一定的仪式后客人和主人在相应的位置投矢，每投中一矢，就放一支算筹（“算”），最后数算筹的多少，就知道大家各投中了多少支矢，然后进行下一步的仪式。在《仪礼》和《大戴礼记》中也用“算”来记录射中或投中的矢的数量。
《孙子兵法》中说“夫未战而庙筭胜者，得筭多也；未战而庙筭不胜者，得筭少也。多筭胜少筭，而况于无筭乎！吾以此观之，胜负见矣。”[42]，其实也是在战前考虑影响战争的各种有利和不利的因素，用算来分别表示对己方和敌方有利的方面，以评估发生战争时可能出现的胜负，从而决定是否出兵或如何出兵。出兵比不出兵“得算多”或我方比敌方“得算多”则能胜，可以出兵，否则不能。这裏的“算”既可以是实际的算筹，也可以指对有利因素的评估值。
《尔雅·释诂》云：“曆、秭、算，数也”[43]。刘徽注《九章算术》“正负术”云：“今两算得失相反，要令正负以名之。正算赤，负算黑。否则以邪正爲异”[44]。意思是：两种数量在性质上得失相反，所以要用正负来命名它们。表示正数的算筹用红色的，表示负数的算筹用黑色的。要不就用摆放位置的正与斜来区别数量的正负。这裏“算”既指算筹，又指用算筹表示的数。
总之，“算”既可以用来表示实际物品的多少，又可以用来量化抽象的事物。
（二）“算”用作考核与评价的计量单位
在居延汉简中，“算”被用作考核与评价的单位。其中有不少竹简中用到“得算”、“负算”。下面是两个典型的例子：
1“甲渠侯鄣：大黄力十石弩一，右渊强一分，负一筭；八石具弩一，右弭生，负一筭；六石具弩一，空上蜚，负一筭；六石具弩一，衣不足，负一筭；坞上望火头三，不见所望，负三筭；
从出土简牍文献看中国早期的正负数概念上望火头二，不见所望，负二筭，□扌□弦一，脱，负二筭；凡负十一筭。”[45]
这裏讲到十石弩、八石弩、六石弩或其他军事设施出现某种问题，要各“负”一算或“负”几算，这些负的算数相加，得到“负十一算”。永田英正先生曾认爲这裏的“算”是一种评价的单位，负一算即减一分[46]。郭世荣先生也认爲这是“在军事检查中因不符合要求被扣分的计算：（－1）+（－1）+（－1）+（－1）+（－3）+（－2）+（－2）=－11”[47]。于振波先生指出：针对不同的东西出现问题都“负一算”，说明不会是减少某件物品，否则减少的东西相加成“凡负十一算”，就会账目混乱。他联繫董仲舒《春秋繁露·考功名》和《九章算术》中的正负数概念，指出汉简中的“得算”、“负算”是考核用语，相当于“加若干分”、“减若干分”[48]。
2“万岁候长充，受官钱，定课四千，负四筭；毋自言堂煌者第一，得七筭。相除，定得三筭。”[49]
郭世荣先生认爲这说明“正负相加：-4+7=3”[50]。
上述两例中“算”是考核与评价的计量单位，相当于“分”。仔细分析起来，可以按两种方式理解。
第一种方式是：如果把“负若干算”解释爲“减若干分”，则与负数概念还是有区别的，因爲“负”字作爲动词，不具有标识数量性质的意义。在第一例中，完全可以理解爲把各种情况下要减的分加起来：1+1+1+1+3+2+2=11，这个结果11就是要减的总分数。而在第二例中，一种情况下减4分，另一种情况下加7分，7和4相减，得到3，由于得的分数7比减的分数4多，所以最后的结果爲得3分。所以，虽然“得若干算”中的“得”（加）和“负若干算”中的“负”（减）是意义相反的两个词，但它们都是动词，既未作爲定语修饰“若干算”而与之结合成名词性词组，也未用来标识后面的数量本身具有正负相反的性质。所以按这种思路，“得若干算”和“负若干算”还不宜直接理解正数和负数概念。不过，有一点值得注意，当把“负”理解爲减时，“凡负十一算”本身虽不具有负数的含义，但如果在某个考核期限内，甲渠侯鄣另外所得总和不到11算，那麽最后的总成绩就只能是负若干算，这意味着这种考核计分以正负数观念爲前提。这种情况是可能的。
第二种方式是：把“得若干算”解释爲得若干（正）分，“负若干算”解释爲记若干负分，这时“得”和“负”就标识了两种数量正负相反的性质，这便意味着古人使用了正负数的概念。
上面第二例中，“相除”二字系指“七算”和“四算”相减而言，正负相反的性质幷没有参与这种运算，因此，按第一种方式理解是说得通的，这时不涉及正负数。如果按第二种方式理解，“得七算”和“负四算”分别相当于（+7）分和（－4）分，那麽“相除”指的幷不是（+7）分和（－4分）相减，而是指计算（+7）分+（－4）分时，先要计算（7分－4分）；“定得三算”就是确定求得的结果3分之性质爲“得三算”。这时正负数的加法通过转化爲两个（正）数的减法，再确定数量的正负来实现。
在居延汉简（包括居延新简）中，“得若干算”和“负若干算”的竹简还有不少，有的情况如上面两条，有的残缺，意义不够明确。另外，敦煌汉简中也有“得若干”、“负若干”的用例，但不与“算”字相连，如1063号简“
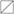
从出土简牍文献看中国早期的正负数概念三负十三 第三负十一 第三负九 第三负七 第三负三 第三负一 第三得二 第三得四
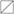
从出土简牍文献看中国早期的正负数概念”[51]。虽然这些简文用到正负数或以默认正负数爲前提的可能性不能排除，但从文本本身幷不能完全肯定其中存在正、负数的明确概念。而正、负数的明确概念，在董仲舒《考功名》和《算数书》“医”条中正好可以看到（详下）。
（三） 董仲舒《考功名》中的考评方法用到正负数概念
上述汉简的例子中，我们还不能肯定意义相反的“得”、“负”具有标识数量正、负性质的功能。而这两个词在董仲舒《春秋繁露·考功名》中则具有标识正、负数性质的功能，分别标识正分和负分。该篇曰：
“考试之法，合其爵禄，幷其秩，积其日，陈其实，计功量罪，以多除少，以名定实，先内第之。其先比二三分，以爲上中下，以考进退，然后外集，通名曰进退，增减多少，有率爲第九。分三三列之，亦有上中下。以一爲最，五爲中，九爲殿，有余归之于中，中而上者有得，中而下者有负。得少者以一益之，至于四；负多者以四减之，至于一；皆逆行。三四十二而成于计，得满计者绌陟之。次次每计，各逐其第，以通来数。初次再计，次次四计，各不失故第，而亦满计绌陟之”[52]。
钟肇鹏先生等引证各家，对文本进行了很好的校释，幷指出陶鸿庆以“其先比二三”中的“二”字爲衍文是正确的[53]。苏舆注云：“计取算法乘除爲名，此爲得负乘除法，未详其式”[54]。“乘除”二字的说法有误，但把“得”“负”和算法联繫起来还是有意义的。于振波先生[55]认爲这段文字把评分和定等联繫起来，提出了一套官吏考评方法。于先生对这段文字进行了总体上相当近真的解释，但还不足以判断其中是否用到正负数概念。现参考于、钟等先生的意见做进一步的解释，幷从语法的角度着重分析和揭示其中“得”、“负”与正、负数概念之间的关係。
董仲舒这段话的意思是，考试的办法，要综合考虑官员的爵位品级、俸禄多少、职位高低、资历深浅、工作实际，计量他的功劳和过错，从功、过两者中的多者内减去少者（即功过相抵），用名号来认证实际，先就单个人定等级。初次考核时分爲上、中、下三等，来考核官员是该升还是该降（“进退”），然后综合全国的官吏来考核，都叫做“进退”，根据情况增减他们的成绩，区分差等，分爲九个档次。这九个档次三行三列排比，原来的每个等次（上、中、下）又各分爲上、中、下三个档次。他认爲各个档次又可以通过相应的数字来体现。最高档爲第一档（“最”），最低档爲第九档（“殿”）。每档都和“中”（第五档）相比较（“有余归之于中”）。也就是说，他把“中”当作一个基点，“中”即第五档对应的分数也正好是“五”。比中好的“有得”，而“得”数有多有少，从一到四，都加到“中”数“五”裏去，便是六、七、八、九；比“中”差的“有负”，“负”也有多有少，“负”数从“负”四开始一直到“负”一，也要和“中”数“五”合幷，合幷的方法是将“负”数变爲减数，也就是分别从“五”中减去四、三、二、一，得到结果一、二、三、四。这些分数一、二、……、八、九，对应于考核的档次第九、八、……、二、一，两者正好相反（“皆逆行”）。
可以看出，“得”和“负”虽然可以从“得到”和“失去”这对相反的意义上来理解，但在“有得”和“有负”中，它们是动词“有”的宾语，已经名词化，应分别理解爲“得的分数”和“负的分数”。因此，这裏的“得”和“负”从形式上讲就可以分别视爲正数和负数。而且，“有得”和“有负”中具有两种相反意义的“得”和“负”，都统一在动词“有”这个概念的基础之上，“有”的作用就是要把“得”和“负”两种数合幷到“中”裏去。“得”数幷入“中”数用“益”（加）的方法：“中”数与“得”数合幷=“中”数+“得”数所得的多少，“得”本身幷不是加法的运算，而转化爲加法运算（“益”），这相当于“（+B）幷入A=A+B”；“负”数幷入“中”数用“减”的方法：“中”数与“负”数合幷=“中”数－“负”数所“负”的多少（相当现代所说的负数之绝对值）。很明显，在这种表述中，“负”本身幷不能直接理解爲减去或减少，“负”某数和“得”某数一样，都是要与“中”合幷，只是“负”某数在与“中”合幷时，要转化爲减以某数，这相当于“(－B)幷入A=A－B”。因此，《考功名》这段文字裏的“得”数相当于正分，而“负”数相当于负分，是正负数概念的应用。这裏涉及正负数观念的如下一些性质：正数和负数相对于同一参照物正好相反，正数与某数（正数）相加就等于两数相加，负数与某数相加等于从某数中减去与该负数相对应的正数（即相反数）。当然，这裏的情形幷不能反映正负数概念的全部内涵，如负数与正数的抽象意义，正数和负数以零爲分隔点，而负数比零小等涵义都没有涉及（正数和负数都是相对于同一个事物而言这一点当然是涉及了的）。
（四）“医”条用到正、负数概念
1“医”条系针对医生治病效果的考核
《周礼》注重统计和会计在国家管理中的作用，其中讲到通过统计医治效果来考评医生成绩的量化标準[56]。其“天官冢宰”云：
“医师掌医之政令，聚毒药以共医事。凡邦之有疾病者、疕疡者造焉，则使医分而治之。岁终，则稽其医事以制其食。十全爲上，十失一次之，十失二次之，十失三次之，十失四爲下。
食医掌和王之六食、六饮、六膳、百羞、百酱、八珍之齐。……
疾医掌养万民之疾病。四时皆有疠疾，春时有痟首疾，夏时有痒疥疾，秋时有疟寒疾，冬时有嗽上气疾。……凡民之有疾病者，分而治之；死终，则各书其所以，而入于医师。
疡医掌肿疡、溃疡、金疡、折疡之祝药、劀杀之齐。……
兽医掌疗兽病，疗兽疡。……凡兽之有病者、有疡者，使疗之；死则计其数以进退之。”[57]
五种医职人员中“食医”、“疾医”、“疡医”、“兽医”是四种专科医生，“医师”则是领导、管理成员，平时负责分派医生，而年终考核专科医生的治病效果，幷据以分配他们的待遇[58]。考核的成绩分5等，最好的上等是“十全”，治10个10个有效；次一点的第二等治10个9个有效；第三等治10个8个有效；第四等治10个7个有效；第五等即下等是治10个6个有效。一般说来，医疗业绩特别好的、好的和较差的医生都应占较少的比例，中等业绩水平的医生比较多，所以第3、4等的医生应该比较多。而政府制定的医生合格标準也应以大多数医生所处的水平爲基準，因此也应接近第3和第4等的水平。
按这种对医生的治病效果进行考核的作法来理解，可以使《算数书》“医”条的问题属性迎刃而解。如上所述，“算”可以指考评打分的单位，“得”、“负”可以指考评打分的正、负（或正分、负分）。那麽《算数书》“医”条中，“程曰：医治病者得六十筭而负廿筭”说的就是，一个医生合格的（最低）标準是：治病后有效的病例占60，而无效和病情加重的病例占20。也就是说，治病的医生要算合格，那麽他的治疗有效和无效（及误治）的比例不低于60比20。“医”条后面的文本，由于竹简保存不好而脱字甚多，详细的涵义虽不太清楚，但残缺尚存的文字“得六十而负几何？曰：负十七筭二百六十九分筭十一。其术曰：以今得筭爲法，令六十乘负筭爲实”说明其中至少讲到一种有效率更高的情形：有效与无效（和误治）的比爲：60比17
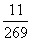
从出土简牍文献看中国早期的正负数概念。
如果我们把“医”条的有效率与《周礼》考核医生业绩的标準做一比较，不难发现两者吻合得相当好。《算数书》“医”条的标準得60算而负20算，相当于治疗10个患者时有7.5个有效，这个标準在《周礼》的第3、第4这两等的正中间，而该条的另一种情况“得60算”而“负17
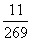
从出土简牍文献看中国早期的正负数概念算”，则相当于治10个患者有7.79个有效，这一有效率稍高，但也在第3和第4等之间而更接近第3等。“医”条的这两种有效率高低适中，比较符合古代人所理解和认同的医术水平。两种文献的惊人“巧合”，说明“医”条确实极有可能是讲考核医生的治病效果的，其中的程就是衡量医生是否合格的量化标準，是战国时秦国（或至迟爲秦代）的法律（笔者将另文详证其时代）。商鞅变法以后，秦国实行了较完善的法律管理体制，睡虎地秦简能在相当大的程度上反映其广度。“医”条中考评医生的量化标準，丰富了这一认识。
2“医”条用到正、负数
考核医生不能光看治好了多少病例或多少病例有效，也不能只看有效病例数减去无效和误治病例数后所得的差，而要看有效率的多少。所以在“得六十筭而负廿筭”一句中，“负廿算”不能理解爲欠、失去、减去20算，而只能把“负”字理解爲标识“廿算”的数量性质的词彙。相应地，“得六十算”中的“得”也只能是一个标识“六十算”的数量性质的词彙。换句话说，“医”条中的“得算”和“负算”就不能分别理解爲加分和减分，而只能分别从正分和负分的角度去理解。“得”、“负”在这一句中可以有两种选择。一种是作定语，分别修饰“六十算”、“廿算”，这时“程曰：医治病者得六十筭而负廿筭”可以理解爲“标準：对治病的医生而言爲：正六十分（有效病例）比负二十分（无效或误治病例）”，显然其中“得”、“负”不仅是表示数量类别的词，而且已经分别和“六十算”、“廿算”结合爲一体，表示两种性质相反的数量。另一种选择是把“得”、“负”理解爲动词，“得六十算”意思是得到六十分（正分），而“负廿算”意思是有负分二十分（而不是失去二十分）。其中“负”字把“廿算”归入与前面（属于“得”类别）的“六十算”性质相反的“负”类别中，这以存在“得的算”（正数）和“负的算”（负数）爲前提。而从语法上分析，可以得知这个“负”字是形容词用如动词，负这种性质实际是和“廿算”结合到一起形成了一个数量的。总之，不论何种理解，这裏都存在具有相反性质的两种数量，因此也就蕴含着正数和负数概念。这样看来，“医”条中的“得若干算”与“负若干算”与它们在居延汉简中的用法在表面上虽然颇爲相似，但在文字本身所表现的数字观念上却可能有着性质上的不同（至少与其中能确认“得”、“负”只分别表示加、减的那些例子相比是如此。）
“医”条后面的文字“得六十而负几何？曰：负十七筭二百六十九分筭十一。其术曰：以今得筭爲法，令六十乘负筭爲实”中，如果说第一个“得”，第一和第二个“负”还可以有如上两种解释的话，那麽第二个“得”和第三个“负”则只能是“算”字的修饰语，表示相应的“算”的性质，也就是说它们标明“得算”和“负算”有正、负相反的两种性质，而这两种性质已经嵌入到数量中去了。因此，“得算”、“负算”应该属于正、负数的範畴。术文包含着乘法和除法：（60×某已知的“负算”）÷已知的“今得算”，其计算结果爲负17
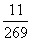
从出土简牍文献看中国早期的正负数概念算。这裏，治病的意义已经在文字中隐去，“得”和“负”作爲标识数量相反性质的两个符号已经和数字结合在一起而形成了性质上正、负相反的两个数量，幷进入到运算中。所以，“医”条不仅确实含有正、负数的概念，而且成功地进行了正、负数的乘除法。
总之，“算”本是用于记数的筹码，一定数量的“算”对应一定的数值，所以也在一定的语境下用于指数量。得到和失去，盈余和不足，债权和债务，有利和有害，胜和负等都各自属于性质相反的一对概念，但古人一般不把这两种相反的性质统一到同一个数量系统中来讨论，因此它们可以是通向正负数概念路径中的一环，而一般不属于正、负数概念。《孙子兵法》“计”篇中战争的胜、负由“算”的多少而不是由“算”的正负相反的性质来判定，充分说明了这一点。在居延汉简表示加分的“得某算”和表示减分的“负某算”中，“得”和“负”对应于两种互逆的运算，但幷不用于描述数量的性质，因此这种用法虽可以视爲通往正负数概念的一环，但本身幷不具有正、负数的基本涵义。董仲舒《考功名》在讲到官吏考评方法时，把相对于同一参照物（“中”）而言性质相反的两种数量“得（的数量）”和“负（的数量）”用于记分，幷且把它们视爲可以合幷的数量，而在合幷时又分别转化爲加法和减法两种运算。因此这裏已经涉及了如何进行正负数加法运算的方法。《算数书》“医”条在考评医生治病有效和无效（或误治）时，使用了“得若干算”和“负若干算”来进行量化。这种量化的方法已经把意义相反的正、负性质嵌入到数概念中幷成爲数量本身的一个部分，因而属于正、负数概念的範围。而“医”条中的计算问题又用到的“负若干算”和“得若干算”的乘除法，则是正负数的乘除运算。

上面说到，现实生活中的得、失相反的两种性质，一般不从统一的同一个数量系统上理解。所以，负数观念的引入，还是需要有一定契机的。在一般情况下，具有得、失相反意义的两种事物，可以分别记录各自的数量。而用数量来判断具有相反意义的两种事物时，还可以用数量的大小作爲依据。如《孙子兵法》就用“得算多”来判断战争的胜，“得算少”或“无算”来判断战争的负。而《考功名》把5作爲中档所对应的分数，通过加分和减分来反映功过，得到不同档次所对应的分数，这时如果不引入正、负数的概念，也完全没有困难。所以一般情况下，要表示得、失相反的两种数量，幷无必要让正、负性质嵌入到数量中形成新型的正、负数概念。例如，无论《算数书》的“医”条、董仲舒还是居延与敦煌汉简，其中涉及的考核都可以把意义相反的两种性质分别开来，用两个不同的类别来表示，数量只描述两类事物的多少，而数量本身幷不涉及这两种性质。因此，正、负数观念的引入在这些考核与评价中幷不是绝对必要的，其中用到正负数的例证幷不属于导致正负数的引入的情形，而属于应用业已産生的正负数概念的情形。另外，《九章算术》的盈不足章有大量盈和不足两种意义相反的数量，如果引入正负数则可使算法简化而更具一般性，但该章幷没有使用正负数概念。出现这种情况的原因，除了该算法的创造时间可能要早以外，它不必要也不足以推动正负数的引进，也是重要的原因。可见，一般意义下的对立相反的两种数量这类观念，幷不能通过自然延伸而过渡到引入正负数的概念，所以作爲数量观念上的重大变革，正负数概念的引入应该是某种必然性因素推动的结果。这种必然性就存在于《九章算术》的方程章中。钱宝琮先生[59]曾指出“‘方程’的每一行是由多项式未知量和一个已知量所组成的等式，其中可能有相反意义的数量，由此産生正数与负数的对立概念。又用‘直除’法消元，减数大于被减数时，也需要负数的概念或扩充减法的功用。因此，中国数学家在方程章裏提出了正、负数的不同表示法和正、负数的加减法则。”可见他也把负数概念的産生归结爲方程算法的需要。不过，以下两方面的理由说明钱先生实际上没有把古代方程算法産生正负数的必然性揭示出来：（1）上面我们已经说明对立相反的意义幷不必然导致负数。（2）钱先生说“所谓‘方程’是联立一次方程组”，幷用代数方程式来解释列出的方程和解法。由于《九章》方程章的问题都是以实际爲背景的，所有问题的答案也都不是负数，所以，问题的答案不会导致负数的産生。而在代数方程式的求解过程中，由于两个式子表示的数量总有一大一小（或相等），所以完全可以在消元时做到从大的数量中减去小的数量（或相等的数量相减），避免不够减而産生正负数的情况[60]。因此，我们有必要分析《九章》方程算法的特殊性来揭示它産生正负数的必然性。
爲了便于理解，我们以方程章第三题爲例来说明方程算法的特点：
“今有上禾二秉，中禾三秉，下禾四秉，实皆不满斗。上取中，中取下，下取上各一秉而实满斗。问上、中、下禾实一秉各几何?荅曰：上禾一秉实二十五分斗之九，中禾一秉实二十五分斗之七，下禾一秉实二十五分斗之四。术曰：如方程，各置所取，以正负术入之。正负术曰：同名相除，异名相益，正无人负之，负无人正之。其异名相除，同名相益，正无人正之，负无人负之。”[61]
古人用算筹来表示数量，我们改用印度—阿拉伯数字代替以适应现代人的习惯。这不会影响我们的分析。如果按符号代数的方法，设上、中、下等禾每秉分别能打出禾实x、y、z斗，那麽列方程组爲：
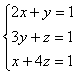
从出土简牍文献看中国早期的正负数概念。古人对应地列出方程如图1-1，其中幷不出现未知量（相当于现代的分离係数），其右、中、左列（古人称爲“行”）分别对应于代数方程组中的上、中、下三个方程式。古代方程的表示法总是把每一个等量关係用一列数表示，不同等量关係中对应于同一个未知量的係数具有相同的前后次序，而对应于常数项的数都放在最后。解方程时，遵循两个原则，一是每一列数各自爲一个整体（刘徽称爲“率”），当其中某个数放大或缩小时，其他的数也要放大或缩小同样的倍数（即一列内的每一个数可以同时乘以或除以同一个数），二是两列数可以相加减，其规则是相应位置上的数分别相加减，而同一列内的数之间不进行加减运算。解方程的目标是使每一列除最后的数（常数项）外，分别只留下一个数（未知项，各列的未知项互不相同）。例如对上面的问题，必须让第1、2、3行都只剩一个数，这就必须通过两列相减（或一列乘一个数与另一列相减，或两列分别乘以两个数后相减）来实现。比如第一行有2个数，我们要消去其中的1个，如果消去右列中的第1个数，那麽从右列中连续2次减去左列，得到的结果如图1-2。这时，右列的第2个数是正数而同时第3和第4两个数就都会是负数。而如果消去左列的第1个数，那麽将左列乘以2再从中减去右列，这时得到的结果如图1-3。这时，左列的第2个必然是负数而第3、4两个数则是正数。不难验证，不论先消哪个元，都会産生正数和负数同时出现的情况。所以，在方程章问题的求解过程中，负数的引入是必然的。
左列
中列
右列

左列
中列
右列

左列
中列
右列

左列
右列
1

2

1





2

7
5

3
1


3
1

-1
3
1

-5
-7
4
1


4
1
-8

8
1


1
1
1

1
1
-1

1
1
1

25
11
图1-1

图1-2

图1-3

图2
但如果我们用字母代数来表示，那麽可用2乘第3式，得到
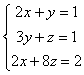
从出土简牍文献看中国早期的正负数概念，以第1式减第3式，得到
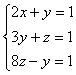
从出土简牍文献看中国早期的正负数概念，这时第三式的“－”完全可以而且应该理解爲减号，而不必用于表示数量的性质。这时第三式实际上对应于图1-3的左列，但幷不需要新型的数（正负数）的参与。虽然也可以由第1式减以第3式从而导致正负数的産生（对应于图1-2的右列），但由于第3式表示的数2比第1式的数1要大，所以这不是人们的自然想法。
上面是解方程过程中的变换必然産生正负数的例子，而方程章第4题则是正负数出现于开始列方程时候的例子：
“今有上禾五秉，损实一斗一升，当下禾七秉。上禾七秉，损实二斗五升，当下禾五秉。问上、下禾实一秉各几何?荅曰：上禾一秉五升，下禾一秉二升。术曰：如方程，置上禾五秉正，下禾七秉负，损实一斗一升正。[言上禾五秉之实多，减其一斗一升，余，是与下禾七秉相当数也。故互其算，令相折除，以一斗一升爲差。爲差者，上禾之余实也。]次置上禾七秉正，下禾五秉负，损实二斗五升正。以正负术入之。”[62]
设上、下禾一秉的实分别爲x、y升，那麽根据题设可以列如下的联立方程组：
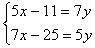
从出土简牍文献看中国早期的正负数概念。“损实某斗某升”即“减去某斗某升的穀子”，它与“当下禾某秉”可以不分别对应于负数和正数。但古代列方程时，古人对方程同一列内的各数字幷不进行加减运算，所以“损实某斗某升”的“损”字，在列方程时幷不能被作爲减法运算来处理，古人就必须通过观念的转换，对所“损”的相应数量进行性质上的认定，具体地的说就是作爲负数来处理，于是这一数量就用“负”字来标记。但是，古人列出的方程必须每一列的最后一个数不涉及未知量，所以在本问题中，古人列方程时要调整有些项的位置，这就需要重新确定那些项的正、负。刘徽注文提出要“互其算，令相折除”，即把下禾（的实）与损的实两个数量交换地位进行相减（“上禾5秉，减去实1斗1升，得到下禾7秉”转化爲“上禾5秉，减去下禾7秉，余下实1斗1升”。同样“上禾7秉，减去实2斗5升，得到下禾5秉”转化爲“上禾7秉，减去下禾5秉，余下实2斗5升”），从而相应改变它们的正、负，这样就对各项重新确定了正负（“上禾五秉正，下禾七秉负，损实一斗一升正”，“上禾七秉正，下禾五秉负，损实二斗五升正”）。于是得到如图2的方程式。
古代不论是在开始列出方程时，还是在对方程进行变换求解的过程中，每一列之内的各数之间幷不相减或相加，因此对每一列之内的各数需要标记的是其正、负的性质，而这种正负的性质幷不能理解爲实际进行的加减运算。而真正在一起参与运算的只是两列的对应位置上的数，这时就涉及了正、负数的算术运算。
在《九章算术》中，不论消元（现代的说法）以后还是开始列出方程的时候，没有数量的项幷不用数值零来刻画，而是空着相应的位置。“正负术”中“正无人负之，负无人正之”（相减的两列中被减列的某个位置空着没有数时，相应的减数就没有对应的数让它去减，当减数是正数时，得数爲负；而当减数是负数时，得数爲正）、“正无人正之，负无人负之”（相加的两列中被加列的某个位置空着没有数时，相应的加数就没有对应的数让它与之相加，当加数爲正数时，得数仍爲正；而当加数爲负数时，得数仍爲负），虽可以用现代的零与正负数相加减来理解，但在原文中不仅没有作爲数值的零概念，甚至对应的项也没有出现。刘徽注云：“无人，爲无对也”，即没有与（一个正数或负数）相配合进行运算的数，这在方程式中就表现爲一个没有摆放数字（算筹）的空位。所以，《九章算术》中正负数概念的引入虽然基于作减法运算时被减数小于减数或没有被减数而出现不够减的情况，而且古人的潜意识裏也有与数值零相对应的观念，但正负数概念的引入却幷不是基于比数值零小的概念。所以刘徽对正负数的界定也不涉及比数值零大还是小这一观念，而是以“得失相反”的性质作爲正负数的核心。
中国古代方程的结构与今天的增广矩阵非常接近，只有竪排与横排之别：古人把每一列各自看作一个整体（按刘徽的说法叫做率），与矩阵的列向量相当；方程的每一列内的数可以放大或缩小同样的倍数，每两列可以相加减（两列对应位置上的数进行加减，结果仍置于相应的位置上），这也与矩阵的列向量的变换相对应。但古代方程每列内的数量不可以拆分开来与其他列内的数量进行重组。这种特殊的结构及相应的运算法则，决定了正负数的必然産生：方程中对应于现代方程组之消元的变换，是以两个整列的对应位置上的数相加减，这就决定了在很多问题的求解过程中必然会出现加减出来的结果有性质相反的两个数的情形。因而正负数概念的引入是不可避免的。由于方程同一列内的各数之间是比率关係，而不是加减关係，这就决定了题设中含有未知量项的相减关係的问题要得到处理，就必然要通过把相减运算转化爲两种数量的意义相反的性质来体现，这种性质必须嵌入到数量中，因而正负数的使用就成爲必然，这样古人在开始列方程时就用正、负数来分别代替被减数和减数。不过，更有可能是从不够减的情形中引入正负数概念以后，使这种处理就变得容易和顺理成章。因此，中国古代的方程不仅在数学史上是具有非凡威力的伟大创造，而且它特殊的结构形式和运算法则也促成了数学史上数量观念的变革。
正负数的概念伴随方程算法而産生，时间应该较早。《周礼·地官司徒》：“保氏掌谏王恶而养国子以道，乃教之六艺。一曰五礼，二曰六乐，三曰五射，四曰五驭，五曰六书，六曰九数”。郑玄（公元127-200年）引郑衆（？-公元83年）注：“九数：方田、粟米、差分、少广、商功、均输、方程、赢不足、旁要。今有重差、夕桀、勾股也”[63]。《周礼》的年代存在很多不同的意见，时间跨度从西周一直至汉初。不过，郑衆所传父亲郑兴之学，源自古文经学派的刘歆，郑衆应是把《周礼》当作爲周代经典看待的。因此，在郑衆的心目中，包括“方程”在内的“九数”，不同于“重差”等汉代才兴盛的数学门类，是周代已有的数学门类。因此，按郑衆的意见，“方程”怎麽说也是先秦的数学门类。堀毅先生曾对比《九章算术》与战国及秦、汉代的物价，认爲《九章算术》与秦及战国接近而与汉代差别较大[64]；郭书春先生在此基础上认爲方程章中属于这种情况的有第7、8、11、17、18五个问题[65]。其中第8、17、18三个问题在术文中都用到了正负数；第11个问题虽没有出现正负数，但术文说要用“损益术”，所以古人在解答过程中肯定也用到了正负数。特别是其中的第17题，羊、犬、鶏、兔的价格分别爲177、121、23、29钱。堀氏找到前二者在汉代的价格分别爲600-1500、500-600钱，这与第17题差距甚大。而二者在秦及战国的价格分别爲220-330、100钱，与第17题很接近。不过，他没有用到居延新简。居延破城子第51号探方223号简记有“出二百五十买羊一，出百八十买鶏五只”[66]，这裏的250钱比他确定的汉代羊价的下限要低很多，但还是高于秦及战国的下限。另外，羊盛産于西北，当时内地的价格应该要比250钱高出不少，比方程章第17题的价格高得更多。此简中的鶏价爲36钱，爲第17题的1倍半还多。而敦煌悬泉《元康四年鶏出入簿》有两支简分别记有“十月尽十二月丁卯，所置自买鶏三只，直钱二百卌，率只八十，唯廷给”（第125号简），“正月尽十二月丁卯置自买鶏十五只一枚，直钱千二百一十五，唯廷给”（第129号简）[67]。此处鶏价都在80钱左右，比第17题的鶏价高了2倍半多[68]。这说明第17题极可能不属于汉代而是更早时代的。可见郑衆的注解、方程章中一些反映先秦物价的问题（包括含有正负数和没含正负数的问题），都说明正负数和方程都应在先秦时代就已经出现。公元前186年以前的《算数书》中的“医”条用到正负数概念，特别是其中引用战国时秦国或秦代的法律含有正负数概念，则正好与此相一致。
七 早期正负数概念与考核评价记录
综合上面的讨论，可以推知：先秦时期的实际生活中存在得与失、赢余与亏欠、多余与不足等相反的情况，爲産生和接受正负数的观念提供了现实的思想基础，先秦时期方程术的産生导致了正、负数的必然引入。而这种观念一旦引入，就可以爲人们所接受和使用。《算数书》“医”条的作者、董仲舒，在幷非必要使用正负数概念的情况下，把已有的正、负数概念用于官吏业绩、医生治病效果等的考核与评价中。居延汉简中含有“得算”、“负算”的大量记录，虽然不能确定其文字本身蕴含着正负数概念，但这幷不意味着其表达方式与正负数概念一定毫无关係，因爲它们同属考核记录，用词与《算数书》“医”条相似，时代也较晚（如有的竹简中记载的王充，是汉元帝建昭时期即公元前38-32年间的人[69]），间接或直接受到过正负数概念的影响是可能的。从上述几种情形推测，在正负数概念産生后的一段历史时期，曾被用于政府部门进行的考核与评价工作当中。之所以如此，推想有两方面因素，一是在战国时代百家争鸣的大环境下，先进的正负数概念容易传播，用于不同的领域；二是考核和评价工作中，往往会涉及正面评价和负面评价两个相反的方面，其思想与正负数概念易于契合。
在《算数书》“医”条中，治病的成败比例已经用更抽象的正负数来描述，纯粹从计算来说当然也很方便。但对实际来说，用正负数却幷不省事，这大概也是我们在后世的材料中没有见到将正、负数用于医生考评工作的原因。由于现存其他文献中见不到汉代官吏考评方法的完整记录，所以我们难以确定《考功名》的方法到底在多大程度上反映了当时的实际。不过，既然“医”条的考评标準中用到正负数概念，董氏的考评方法如果不用正负数概念而只用加减概念，也不会存在什麽困难，所以《考功名》也不太会是突如其来地使用正负数概念的，而可能与当时或此前的考评工作中已有正负数概念的应用有关，它亦可能影响到当时或之后实际考评工作中正负数概念的使用。另外一个值得注意的现象是，《考功名》虽然也用到“得”和“负”这样意义相反的词，但以5（而不是0或其对应物）爲基準，且不出现“算”字，呈现出与“医”条（或许还有居延、敦煌汉简中某些用例）中正负数观念的应用不同的特点。这说明董仲舒关于正负数的思想幷不是照搬了以“医”条爲代表的一类正负数观念，很可能作爲一代大儒的董仲舒自身具有相当丰富的数学知识，在当时考评工作已用到正负数的背景下，将正负数概念通过自己的方式引入到考评方法中；或者当时已在一定的範围内，形成了使用正负数进行考评工作或设计考评方法的另一种方式。有意思的是：如果都不用正负数概念，《算数书》“医”条把医疗分爲有效与无效（或误治）两类，数量只记录其绝对数的多少而不反映数量的正负性质；《考功名》则只用加减运算而不涉及数量的正负，那麽古人同样可以解决相应的问题。可见，正负数的介入在这类考评工作中幷没有特别明显的优势。所以，正负数概念的核心内涵在居延汉简涉及考评的“得若干算”、“负若干算”用例中没有明显的体现，现存后代文献中也没有见到考评分等中用到正负数概念，这是不奇怪的。另外，意义相反本是现实存在、思维中容易理解的性质，而在《算数书》“医”条中，正、负数概念直接与医疗成败两种相反的情况对应；在《考功名》中正、负数概念参与运算时直接和加、减发生相应的转换。这类把正负数与数字运算及其他事物相对应的观念一直有形或无形地存在于中国传统数学着作中，这大概是中国古代长期使用负数，却没有如欧洲那样，总是责问负数合法性的原因之一。
总之，得和失（负）、有和无等现实生活中存在着的意义相反的观念，爲正、负数的産生提供了思维背景。而正、负数的正式引入乃是由于方程算法中不可避免地要出现正负相反的两种数字。这种正、负数和方程算法应出现于先秦。正负数观念産生以后，爲一些管理者和学者所接受，用于考核与评价等问题中，原来在现实生活中存在着的得失、利害、盈亏等对立相反的观念，成爲接受正、负数概念的背景思想。不过，对于这些实际工作来说，古人对正负数的理解仅限于性质相反的两种数量这一认识深度就足够了，而不太必要与0观念一起清晰地统一到一个数系中去。所以，从由浅入深的认识论来说，居延汉简中表示加分的“得算”、表示“减分”的“负算”，《考功名》和“医”条中正、负数的观念虽然可以视爲向方程算法中的正、负数概念发展的一个环节，但从历史实际的角度看，情况却很可能是反过来的：正、负数概念在方程算法的直接推动下産生以后，曾影响到政府的考核和评价方法，《考功名》和“医”条对正、负数概念的应用正是这种影响的表现（居延汉简的“得若干算”、“负若干算”也有可能受此影响，但仍有很大的可能性是原有的两种事物性质相反这一观念的继承或发展），是原有的两种事物性质相反这一观念（盈与不足，得与失，成功与失败，债权与债务等）与新生的正、负数概念（对立相反的性质嵌入到数量中成爲数量本身的一部分，幷可以进行运算的数量）结合到一起的结果。
八 余论——关于方法论的初步讨论
对于研究科学史的学者来说，我们总是希望能够有充分的证据建立对某一科学上的事物、事件和思想的历史性认识。但建立这种认识时，我们往往幷没有足够的幸运见到足够丰富的资料。不过，有时候仔细关注和分析科学问题的特殊性在材料中的表现，也能从很有限的材料中获得相当多的信息。这种分析不仅需要眼光，也需要方法。眼光来自素质、知识和训练的综合作用，它虽然重要，却难以捕捉和言传；方法则有规矩可循。所以，这裏笔者就有关的方法论问题做一简单的讨论。
由于古人对概念和用语的涵义通常不做定义或明确的界定，我们一般只能从上下文来判断。从便于现代知识背景的人理解古代的事物和思想的角度来说，用传统的释词方法根据上下文来解释在大多数情况下是足够的，甚至对于语言学上的一般性研究来说可能也够了，有时也许还是一种好的选择。因爲通常的字典、词典解释字词，不可能义项太多，每个义项需要一定的包容度；而在一般的古籍注释中，大致的描述或告诉读者古代某个东西在现代的对应物，也能满足需要。但这种释词方法不太注意限定内涵和外延的範围，容易失之宽泛和模糊。这对于我们认识某个概念的本质属性来说，有时是不够的。因爲概念的本质特徵，有时是从细微处体现出来的。因此，我们还需从更近的距离着眼，查看相关的词彙有哪些，考察古人通过何种方式建立需要解释的词彙与这些词彙之间、这些词彙彼此之间的联繫，形成什麽样的结构，各词、词组起什麽样的语法功能，等等。这样，不仅能较好地确定各词彙和术语的涵义，而且能较好地了解整个词组和句子的涵义，进而把握古人的思想。
科学概念和思想的演变与发展，有其内在的逻辑，但对这种逻辑不能简单地按从低到高、从简到繁来理解，更不能通过把现存史料中所反映出来的相关信息简单地按这种次序来描述。我们既需要分析科学概念和思想産生和发展的背景和因素是什麽，其中何种因素是关键性和决定性的；也需要根据史料本身所映的情况及史料的时间顺序来考虑问题。既尊重史料和历史的複杂性，也充分兼顾科学概念和思想演化的内在逻辑。这样才能有利于我们对所研究的对象获得一个接近历史真实的认识。
本文所讨论的问题，主要涉及以下几个关键点。
1．“算”字的各项意义在特定的语境中究竟哪一项合适。
2．人类对正、负数概念的认识是一个历史的过程，何种情况可以视爲形成了正、负数概念。换句话说，正、负数概念最核心的涵义是什麽。
3．怎样判断某项文献用到正、负数概念的最核心的涵义。
4．産生正、负数概念需要何种动因。
5．各条文献中使用了正、负数概念的情况，分别处于历史进程中的何种位置。
在第2和第4两个关键问题上，笔者主要从历史的角度和数学知识本身的特点进行分析来阐释和判断。在这裏，知识结构的观念十分重要。对知识结构观念的準确把握，不仅有助于理解一种知识的本身，而且有助于认识这种知识的功能（结构的性质也部分地体现在功能上），了解它的发展趋向。例如对第4个问题来说，正负数概念虽然以现实中的盈亏等意义相反的性质爲背景，但这类背景材料很多，其中绝大部分所包含的知识的结构都不足以推动数量观念的变革，只有其中的方程算法这种特殊的知识结构才必然带来数量观念的变革，导致正负数观念的産生。而刘徽关于《九章》成书过程的记载、郑衆对《周礼》“九数”的注解加上物价方面的证据，正好可以解释正负数産生于《算数书》“医”条之前这一时间上的问题。对于第1、3、5三个问题，则除了从这两方面考虑外，还特别倚仗语言分析的方法。在第1个问题上，不仅各个词彙的涵义、整个文本的意义需要考虑，而且需要与其他相关文献的记录进行对比分析，从逻辑上统一和实际上符合两个方面的要求来决定“算”字的何种意义是最爲合理的，幷进而阐释整个文本的意思。其中，语法分析起了重要的作用。例如作爲动词的第（3）、（4）、（6）三个义项，因爲词性不合可以马上排除。在“医治病者得六十筭而负廿筭”中，“医治病者”爲主语，统领“而”字联接的两个词组“得六十算”和“负廿算”，其中两个“算”字的意义应该相同。而作爲税钱单位的第（5）个义项，则会导致医生既收税又缴税，这既有逻辑上的矛盾，也与实际不符。而林仓亿由义项（5）发展而来的义项“钱的单位”，则既于史无征，也同样导致与实际不符的情况。而第（1）个义项算筹，由于实物不同于事情，自然也要排除。只有第（2）个义项“数量”、“数目”，从语法、语义和逻辑上都能说通，但也不能笼统地理解，而应参照居延汉简、《考功名》中有关考核记分的情况，以及与《周礼》关于对医生进行考核的记录等，把“算”字在具体的语境中释爲考核评价时的计分单位。
在讨论第3个问题时，重要的是弄清文本是否具有正、负数的核心涵义“性质相反的两种数量”。爲了达到这一目的，通过语法分析可以厘清“得”、“负”与“若干算”之间的关係，“得”、“负”的语法功能，以确定词组“得若干算”和“负若干算”在不同文献中的真实涵义，从而可以判定很多用例（不是全部，毕竟材料本身的局限性不是总能克服的）中古人是否用到了正、负数的概念。这样就克服了平常解释文本时容易模糊不同概念的界限的毛病。用这种方法笔者不仅区分了“得（若干）算”、“负（若干）算”在《算数书》“医”条中与在居延汉简中有不同之处，而且通过对“有得”、“有负”进行语法分析也能判定《考功名》用到了正、负数概念。这样结合《九章算术》方程章中正负数、物价方面的证据，以及郑衆对《周礼》“九数”的解释等文献，我们就能较好地回答第5个问题，幷由此获得关于中国上古时代正负数观念发展的一个历史性的认识，它既符合数学观念産生和传播的内在逻辑，又能兼顾文献的特点和时代顺序。
附记：本研究得到国家自然科学基金项目“《算数书》与先秦数学”（项目类别：A，批准号：10171107。）的资助，本文修改稿得到中国科学院自然科学史研究所中国古代科技史前沿课题“简牍与上古数学史研究”的资助。日本张家山汉简“算数书”研究会田村诚博士专门给笔者把该会编着的《汉简“算数书”——中国最古の数学书》中解释“医”条的篇章译成英文，使笔者对他们的工作有相当的了解。在此谨向田村诚博士致以深切的谢意。
The Concepts of Positive and Negative Numbers of in Early China: A Research Based on the Unearthed Bamboo and Wooden Slips
by ZOU Dahai
(Institute for the History of Natural Sciences, CAS)
Abstract Through the analysis of the contents related to the official evaluations in the unearthed documents with the references of the historical literature, some misunderstandings to the concepts of positive and negative numbers in ancient China could be corrected and the early history of the concepts of the positive and negative numbers could be constructed. This paper pointed out that the standard to judge if the ancient people used the concepts of positive and negative numbers is that the opposite natures were grafted into amounts and became parts of the amounts; argued that the character Suan 算 in Yi医 （the Doctor）entry of Suanshu Shu算数书 （Writings of Reckoning）could not be a tax unit or a currency unit in general meaning and this entry was neither for the income and tax of a doctor practicing medicine nor for the earning and cost. This paper proved that the Yi entry was the rules defining the lowest ratio of successes to failures of a qualified doctor’s treating cases, and the Suan was the scoring unit for assessing the effects of the treatments of the doctor. By grammatical analyses, this paper proved that the concepts of positive and negative numbers do have been applied in the Yi entry of Suanshu Shu and the Chapter “Kao Gong Ming考功名 (Appraise Achievement and Official Position)” in Chunqiu Fanlu (Luxuriant Dew of the Spring and Autumn Annals) by Dong Zhongshu; however, those suspected cases seen in the bamboo and wooden slip documents unearthed from the sites of Han Dynasty in Juyan and Dunhuang are still waiting for confirmation because of insufficient information. This paper argues that the opposite meanings such as gains and losses, successes and failures, etc. were indeed the foundations for the concepts of positive and negative numbers, but the special structure of the Fangcheng (juxtaposed examinations of standards) algorithm in Pre-Qin Period was the decisive factor to prompt the emergence of these concepts. The new concepts of positive and negative numbers influenced the evaluation and examination methods to the officials, the traces of which could be seen in the Yi entry of Suanshu Shu and the Chapter “Kao Gong Ming” in Chunqiu Fanlu (possibly including some contents of the bamboo and wooden slip documents of Juyan and Dunhuang). This paper also analyzed the features of using concepts of positive and negative numbers in these assessing methods. At the end, this paper gave a preliminary discussion to the research methods and emphasized the importance of grammatical analyses and the idea of knowledge structure.
Key words: concepts of positive and negative numbers, Yi entry of Suanshu Shu, Fangcheng method in the Nine Chapters on Mathematical Procedures, Kao Gong Ming of Chunqiu Fanlu, documents on bamboo and wooden slips, Early history of mathematics in China, method of official evaluations and examinations in Early China, research methods of grammatical analyses and structure analyses．　
网上发表附记：
本文已刊印于《考古学报》2010年第4期第481-504页。但该版本有一些编印问题。本网络版做了恢复幷偶有修改，较爲完整。又，刊印版本的英文摘要是《考古学报》编辑部组织专家根据我提供的中文摘要翻译的，但杂志只有英文摘要。现稍作校订，将中、英文摘要一幷纳入,幷补上关键词。（邹大海 2010年11月30日）
（编者按：[1]李俨：《中国古代数学史料》，4页，科学技术出版社，1956年。
[2]郭世荣：《汉简屯戍记录中的实用数学》，《内蒙古师大学报（自然科学）》1989年1期增刊，50—57页；郭世荣：“负数的例子”，见李迪主编《中国数学史大系 第一卷 上古到西汉》，352—354页，北京师範大学出版社，1998年。
[3]永田英正对这一问题，有两种不同的意见。他早年认爲这些用例中的“算”是一种评价单位，“负一算”即减一分。见永田英正着，姜镇庆译：《论礼忠简与徐宗简》，《简牍研究译丛》第二辑，35—57页，中国社会科学出版社，1987年。永田英正后来认爲“负若干算”是器物减少若干件的意思。见永田英正着，谢桂华译：《居延汉简集成之二——破城子出土的定期文书（二）》，《简牍研究译丛》第二辑，58—163页，中国社会科学出版社，1987年。
[4]于振波：《汉简“得算”、“负算”考》，《简帛研究》第二辑，324—331页，法律出版社，1996年。
[5]邹大海：《中国数学的兴起与先秦数学》，155—156页，河北科学技术出版社，2001年；邹大海：《出土〈算数书〉初探》，《自然科学史研究》2001年3期，193—205页；邹大海：《睡虎地秦简与先秦数学》，《考古》2005年6期，57—65页。
[6]邹大海：《出土〈算数书〉初探》，《自然科学史研究》20卷3期，193—205页。
[7]郭书春：《〈筭数书〉初探》，《国学研究》十一卷，324—325页，北京大学出版社，2003年。
[8]王建青、张新立：《〈算数书〉中的记数方法》，《自然科学史研究》2005年3期，224—225页。
[9]Cullen, Christopher, The Suàn shù shū 筭数书 ‘Writings on reckoning’: A translation of a Chinese mathematical collection of the second century BC, with explanatory commentary, Needham Research Institute Working Papers: 1, Cambridge: Needham Research Institute, 2004. p61.
[10]林仓亿：《漫谈〈算数书〉（一）：从“医”开始》，《HPM通讯》2005年6期，2—5页。
[11]马彪：《张家山汉简〈算数书〉的国际性探讨——〈算数书〉及相关简牍国际讨论会：台北（2006）综述》，《HPM通讯》2006年12期，1—5版。
[12]张家山汉简『算数书』硏究会编：《汉简『算数书』——中国最古の数学书》，85—87页，朋友书店，2006年。
[13]李俨：《中国古代数学史料》，4页，科学技术出版社，1956年。第一个“正整数”可能是排印错误或作者的笔误。
[14]张家山二四七号汉墓竹简整理小组编着：《张家山汉墓竹简[二四七号墓]》，释文注释258页，文物出版社，2001年。
[15]何有祖：《张家山汉简〈脉书〉、〈算数书〉札记》，《江汉考古》2007年1期，91—93页。
[16]林仓亿：《漫谈《算数书》（一）：从“医”开始》，《HPM通讯》2005年6期，2—5页。
[17]张家山二四七号汉墓竹简整理小组编着：《张家山汉墓竹简[二四七号墓]（释文修订本）》，141—142页，文物出版社，2006年。
[18]Cullen, Christopher, The Suàn shù shū 筭数书 ‘Writings on reckoning’: A translation of a Chinese mathematical collection of the second century BC, with explanatory commentary, p61-62.
[19]许慎：《说文解字》，99页，中华书局，1987年。
[20]段玉裁：《说文解字注》，198页，上海古籍出版社，1992年。
[21]中国社会科学院语言研究所词典编辑室编：《现代汉语词典》，1305页，商务印书馆，2005年。
[22]“算”爲成年人头税的说法幷不準确。因爲上了一定岁数的老年人幷不需要交算赋，开始交算赋的年龄也在不同时期有所变化。如顔师古注《汉书·高帝纪》载汉高帝四年“八月，初爲算赋”时引如淳曰：“《汉仪注》民年十五以上至五十六出赋钱，人百二十爲一算，爲治库兵车马。”（班固撰，顔师古注：《汉书》，46页，中华书局，1990年）。《汉书·贡禹传》载汉元帝时贡禹曾请求改爲“宜令儿七岁去齿乃出口钱，年二十乃算”（班固撰，顔师古注：《汉书》，3075页，中华书局，1990年）。我以爲“成年劳动力人头税”是“算”的一个比较準确的现代解释。
[23]宁可：“算赋”，见中国大百科全书总编辑委员会《中国历史》编辑委员会、中国大百科全书出版社编辑部编：《中国大百科全书·中国历史（缩印本）》，654页，中国大百科全书出版社，1994年。
[24]这样解释显然不符合语法。古克礼先生曾提出两种他不太确定的可能性：政府向医者徵税或政府付给他钱。见Cullen, Christopher, The Suàn shù shū 筭数书 ‘Writings on reckoning’: A translation of a Chinese mathematical collection of the second century BC, with explanatory commentary, p61.
[25]《汉书·惠帝纪》载惠帝六年：“女子年十五以上至三十不嫁，五算”。应劭注曰：“汉律人出一算，算百二十钱。唯贾人与奴婢倍算。今使五算，罪谪之也”（班固撰，顔师古注：《汉书》，91页，中华书局，1990年）。可见，贾人只交2算的成人劳动力人头税，就算是偏重的；至于爲了增殖人口，女子到了年龄不嫁要缴5算，就是很大的惩罚。很难想像在常规状态下，要对医生徵收几十算的算赋。
[26]班固撰，顔师古注：《汉书》，152页，中华书局，1990年。
[27]范晔撰，李贤等注：《后汉书》，2018—2019页，中华书局，1973年。
[28]甘肃省文物考古研究所、甘肃省博物馆、文化部古文献研究室、中国社会科学院历史研究所编：《居延新简》，476页，文物出版社，1990年。
[29]例如徐中舒主编：《汉语大字典》第6册（3623—3624页，四川辞书出版社、湖北辞书出版社，1989年），罗竹风主编：《汉语大词典》10卷（62—63页，汉语大词典出版社，1992年），广东、广西、湖南、河南辞源修订组、商务印书馆编辑部编纂：《辞源》（修订本1-4册合订本）（1602-1604页，商务印书馆，1995年），王力主编：《王力古汉语字典》（1321页，中华书局，2002年），辞海编辑委员会编纂：《辞海》（1999年版缩印本）（1326页，上海辞书出版社，2000年）中“负”字都有亏欠义，而无缴纳义。
[30]张家山二四七号汉墓竹简整理小组编着：《张家山汉墓竹简[二四七号墓]（释文修订本）》，202页，文物出版社，2006年。
[31]张家山二四七号汉墓竹简整理小组编着：《张家山汉墓竹简[二四七号墓]（释文修订本）》，150页，文物出版社，2006年5月。
[32]据《算数书》“程禾”条，黍一石爲16
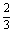
从出土简牍文献看中国早期的正负数概念斗。如按小石即10斗计，一石只15钱，三百石官员的常俸还会低得多。
[33]班固撰，顔师古注：《汉书》，721页，中华书局，1990年。
[34]黄今言：《秦汉商品经济研究》，227-228页，人民出版社，2005年。
[35]黄惠贤、陈锋主编：《中国俸禄制度史》（修订本），36—45页，武汉大学出版社，2005年。
[36]黄惠贤、陈锋主编：《中国俸禄制度史》（修订本），59—61页。
[37]“医”条的“医治病者”，是很宽泛的的表述。从以《算数书》随葬的墓主的情况、《算数书》其他条目涉及的社会经济等多方面看，“医”条中的医生服务于高级部门的可能性极小。
[38]高敏着：《秦汉史探讨》，310—315页，中州古籍出版社，1998年。
[39]班固撰，顔师古注：《汉书》，1181页，中华书局，1990年。
[40]邹大海：《中国数学的兴起与先秦数学》，32—37、70—72，95—102页，河北科学技术出版社，2001年。
[41]孙希旦撰，沈啸寰、王星贤点校：《礼记集解》，1383—1394页，中华书局，1989年。
[42]李零：《吴孙子发微》，30页，中华书局，1997年。
[43]周祖谟：《尔雅校笺》，20页，云南人民出版社，2004年。
[44]郭书春：《〈九章算术〉汇校本》，388页，辽宁教育出版社，1990年。
[45]谢桂华、李均明、朱国照：《居延汉简释文合校》，90页，文物出版社，1987年。
[46]永田英正着，姜镇庆译：《论礼忠简与徐宗简》，《简牍研究译丛》第二辑，35—57页，中国社会科学出版社，1987年。
[47]郭世荣：《汉简屯戍记录中的实用数学》，《内蒙古师大学报（自然科学）》1989年第1期增刊，50—57页。
[48]于振波：《汉简“得算”、“负算”考》，刊《简帛研究》第二辑，324—331页，法律出版社，1996年。
[49]谢桂华、李均明、朱国照：《居延汉简释文合校》，319页，206.4号简，文物出版社，1987年。
[50]郭世荣：《汉简屯戍记录中的实用数学》，《内蒙古师大学报（自然科学）》1989年第1期增刊，50—57页。
[51]甘肃省文物考古研究所编：《敦煌汉简（全二册）》，260页，中华书局，1991年。
[52]钟肇鹏：《春秋繁露校释（校补本）》，411页，河北人民出版社，2005年。
[53]钟肇鹏：《春秋繁露校释（校补本）》，411—415页，河北人民出版社，2005年。
[54]苏舆撰，钟哲点校：《春秋繁露义证》，181页，中华书局，1992年。
[55]于振波：《汉简“得算”、“负算”考》，刊《简帛研究》第二辑，324—331页，法律出版社，1996年。
[56]参考邹大海：《中国数学的兴起与先秦数学》，79页，河北科学技术出版社，2001年。林文也引及《周礼》中考核医生的史料，以佐证“医”条系讲考核医生的可能性，但未加深察，以致在“医”条是讲收税还是讲考核的问题上摇摆不定。
[57]孙诒让撰，王文锦、陈玉霞点校：《周礼正义》（全十四册），315—340页，中华书局，1987年。
[58]四种专科医生中，上述文献中只提到疾医要把死者死亡前的病症上报医师，兽医要统计死亡的数目幷据以决定其升降。显然这裏提到的远比专科医生应该报告给医师的信息要少。
[59]钱宝琮主编：《中国数学史》，55页，科学出版社，1981年。
[60]李继闵先生认爲“（方程解法中普通使用的）直除是以少行减多行，而这个限制常常使方程术无法畅行”，“导致了正负数的産生”。他还指出近代的方程理论以等量关係爲基础，中国古代的方程以比率关係爲基础。如果把中国古代的方程理解爲近代的方程，那麽针对古代只有正数解的实际问题，古人完全可以避免引入正负数。他以《九章》方程章第三问爲例，具体说明如按近代方程来理解古人的方程可以避免正负数的引入。这比钱先生又进了一步。但他对古人解题时必然引入正负数，幷没有具体的分析和论证。文见：李继闵：《〈九章算术〉与刘徽注中的“方程”理论》，载吴文俊主编《〈九章算术〉与刘徽》，274—294页，北京师範大学出版社，1982年。
[61]郭书春汇校：《〈九章算术〉汇校本》，388—389页，辽宁教育出版社，1990年。“无人”的“人”字爲底本文字，《汇校本》改爲“入”字。今仍从底本。理由见郭书春译注：《九章筭术译注》，73—74页，上海古籍出版社，2009年。
[62]郭书春汇校：《〈九章算术〉汇校本》，389—390页，辽宁教育出版社，1990年。括号内的字是刘徽注。
[63]孙诒让撰，王文锦、陈玉霞点校：《周礼正义》（全十四册），1010页，中华书局，1987年。
[64]堀毅：《秦汉物价考》，见《秦汉法制史考论》，268—306页，法律出版社，1988年。
[65]郭书春：《张苍与〈九章算术〉》，《科史薪传——庆祝杜石然先生从事科学史研究40周年学术论文集》，112—121页，辽宁教育出版社，1997年。
[66]中国简牍集成编辑委员会：《中国简牍集成》第十册，98页，敦煌文艺出版社，2001年。
[67]胡平生、张德芳撰：《敦煌悬泉汉简释粹》，78页，上海古籍出版社，2001年。
[68]胡平生先生等认爲“双”（双）习惯省写爲“只”（只），凤凰山167号汉墓遣册凡言“只”者，出土实物多爲“双”。见胡平生、张德芳撰：《敦煌悬泉汉简释粹》，79页，上海古籍出版社，2001年。第17题虽未提及鶏的单位，但如果双是常用的单位，则该题的鶏价似亦应指双而言。这时，各种文献中鶏价相差的倍数亦应不变。
[69]李振宏、孙英民着：《居延汉简人名编年》，156—157页，中国社会科学出版社，1997年。 (责任编辑：admin)

原文出处：http://his.newdu.com/a/201711/05/514016.html

以上是关于从出土简牍文献看中国早期的正负数概念的介绍，希望对想了解历史故事的朋友们有所帮助。