《张家山汉简〈算数书〉》“大广”脱字补 ,对于想了解历史故事的朋友们来说，《张家山汉简〈算数书〉》“大广”脱字补是一个非常想了解的问题，下面小编就带领大家看看这个问题。

原文标题：《张家山汉简〈算数书〉》“大广”脱字补

（上海）
本文摘要：本文利用《九章算术》求田亩解法和初级代数的方法，结合一次同余式的解法，对张家山二四七号汉墓竹简《算数书》“大广”一篇的脱文进行了勘补，并对该简文已释文字中的讹错点进行了勘误。
关键字：张家山汉墓竹简 算数书 脱字 一次同余式
张家山二四七号汉墓竹简《算数书》“大广”原文两简，第一简前几字模糊不清。经整理小组辨识，整理出的内容两简全文如下：
大广 广七步
《张家山汉简〈算数书〉》“大广”脱字补九分步之□□□□□□□□□□□□□□□□□为□六十四步有（又）三百
《张家山汉简〈算数书〉》“大广”脱字补三分步之二百七十三。大广术（术）曰：直（置）广从（纵）而各以其分母乘其上全步，令分子从之，令相乘也为实，有（又）各令分母相乘为法，如法得一步，不盈步以法命之。
该段文字的内容和术文翻译成现代汉语（为描述和计算方便，文中数字用阿拉伯数字代替），意思大致是：
广7又49分之□步，求纵□又□分之□步的情况下其田亩面积。答案是64又343分之273（平方）步。计算法（大广术）：将广和纵带分数的分母分别乘以各自的整数部分（全步），再加上带分数各自的分子部分。将广和纵如此计算后的所得再相乘，作为被除数（原文需补上逗号为：令相乘也，为实），再将各自的分母相乘，作为除数（又各令分母相乘，为法）。整理乘得的被除数（实）和除数（法），用除数去除被除数，被除数每满除数就进一（如法得一步），直到被除数只剩下不足除数的部分（不盈），以除数作为分母，被除数不足除数的部分作为分子（命之）。
术文计算过程其实就是将广和纵两个“带分数”值（由一个整数和一个真分数组成，数值大于1的最简分数）演变成“假分数”值（分子大于或等于分母，数值大于或等于1的分数），再将两个假分数的分子和分母分别相乘，其中分子相乘所得作为被除数，分母相乘所得作为除数。用除数去除被除数，被除数被分成两个数，一个是除数的整数倍数，一个是分子小于除数、分母为除数的真分数。
正如唐李淳风注所说：“大广田者，初术直有全步无余步，次术空有余分而无全步，此术先见全步复有余分，可以广兼三术，故曰大广。”整理小组只引用了这段注[1]，可惜并没有根据这个思路去推究出该简文所脱部分究竟是什么文字和数位元。到该书修订本2006年出版时该处脱文依旧[2]。
现借助代数法推求该段文字所脱部分。
设“广7步49分步之□□□”所脱部分为A，按照文意计算，“广”演变成假分数后的分子为(7×49+A)，分母依然是49。
又设所脱“纵”的整数部分（全步）为B，真分数部分的分母为D，分子为C。显然，这些代数均为正整数。
根据文意，可知：
（7+A/49）×（B+C/D）=64+273/343 （式1）
术文意即：

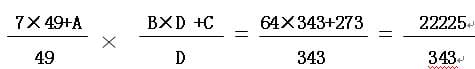
《张家山汉简〈算数书〉》“大广”脱字补
这裏，（7×49+A）×（B×D+ C）即为“实”，而49×D为“法”。根据术文，广之分母49乘以纵之分母，得“法”为343。
即49×D ＝343，得：D＝7。
由于A在广的带分数运算式中是分母49的分子，C在纵的带分数运算式中是D的分子，根据真分数的分子小于分母的特性，则A和C的定义域分别为：
A： 1≤A≤48的整数； C： 1≤C≤6的整数。
将D＝7代入式1：（7+ A/49）×（B+ C/7）＝64+273/343 （式2）
整理得：（7+ A/49）×B +（1+A/343）×C ＝64+273/343
则：B ＝（64×49+39）/（A+343）-C/7
B ＝ 3175/（A+343）-C/7 （式3）
A ＝ 3175/（B+C/7）-343 （式4）
C ＝ 22225/（A+343）-7B （式5）
由式3可知，B与A和C成负相关。当A和C取最大值时，则B为最小值；A和C取最小值时，则B为最大值。
当A＝48，C＝6时，B＝3175/391-6/7≈7.26。
当A＝1，C＝1时，B＝3175/344-1/7≈9.09。
即7.26≤B≤9.09。因为B是整数，所以，B＝8，或B＝9。
即该简原文第一句似乎应为：
“广七步
《张家山汉简〈算数书〉》“大广”脱字补九分步之□□□纵八（或九）步七分步之□，为田六十四步有（又）三百
《张家山汉简〈算数书〉》“大广”脱字补三分步之二百七十三。”
至此问题似乎已经变得很简单，因为只要分别将8或9分别代入以上式中，即可轻鬆推导出A和C这两个整数来。
将B＝8代入式4，则：A＝3175 /（8+ C/7）- 343 （式6）
因为1≤C≤6，分别取C＝1、C＝2……C＝6值，代入式6，得：
C值
C=1
C=2
C=3
C=4
C=5
C=6
A值
46.91
40.19
33.69
27.41
21.34
15.47
均不符合A为整数的要求。故B=8不可取。
同样，将B=9代入式4，则：A ＝3175/（9+C/7）-343 （式7）
因为1≤C≤6，分别取C＝1、C＝2……C＝6值，代入式7，得：
当C＝1时，A＝4.27；C取2至6值时，A均小于0，A同样无正整数解。故B＝9亦不可取。
可见，据该文所提供资料进行推导，在数理上无解。说明整理小组所给图版释文中的几个数字肯定有讹错。哪个数有问题呢？
查看《张家山汉墓竹简》该段图版得知[3]，“大广”该段的“有（又）三百
《张家山汉简〈算数书〉》“大广”脱字补三分步之二百七十三”是清晰无疑的，但“六十四步”的“四”并不清晰，上述推倒悖论应是该数字出了问题。现设该数字为E，因为它是“六十□步”的个位数，显然，E的定义域为：
E： 1≤E≤9的整数。
则式2～式5分别应为：
（7+ A/49）×（B+ C/7）＝60+ E +273/343 （式8）
经整理得：
（343+ A）×（7B+ C）＝343×（60+E）+273
此式相当于一个一次同余式：
（343+ A）×（7B+ C）≡273（mod 343）
目前仅知A和C的定义域（前文所述），B定义域不明，需推求。
根据式8，有：B ＝[（60+ E）×49+39]/（A+343）- C/7
B ＝（2979+49E）/（A+ 343）- C/7 （式9）
A ＝（2979+49E）/（B+ C/7）- 343 （式10）
C ＝（2979+49E）×7/（A+343）-7B （式11）
根据上述四式，分别推求A、B、C的取值範围：
首先看B：
由式9可知，B与A、C和E的数值关係为：
当A和C取最大值，且E取最小值时，B为最小值；
当A和C取最小值，且E取最大值时，则B为最大值。
即当A＝48，C＝6，E＝1时，B是最小值，根据式9，有：
B＝（2979+49×1）/（48+343）-6/7≈6.89
当A＝1，C＝1，E＝9时，B是最大值，根据式9，有：
B＝（2979+49×9）/（1+343）-1/7≈9.80
因此，B的定义域应为“大于6.89，且小于9.8的正整数”，即：
B值只有7，8或9这三种可能。
再看A：
整理式10，A＝（2979+49E）/（B+C/7）-343
＝7×（2979+49E）/（7B+C）-7×7×7
＝7×[（2979+49E）/（7B+C）-7×7]
注意上式中的7B+C，是7的倍数加上C，因为C小于或等于6的整数，不可能是7的倍数，所以7B+C不可能被7整除，因此A必然是7的整数倍，又因A定义域是1≤A≤48的整数，则：
A有7，14，21，28，35和42这六种取值可能。
再令A＝7a,显然a定义域是1≤a≤6的整数。则式8变更为：
（7+ 7a/49）×（B+ C/7）＝60+ E +273/343 （式12）
再看C：
将A=7a代入式11，有：
C＝（2979+49E）×7/（7a+343）-7B
＝（2979+49E）/（a+49）-7B（式13）
因C定义域为1≤C≤6的整数，则上式：
1≤（2979+49E）/（a+49）-7B≤6 （式14）
再根据上述各数值定义域和数值之间的相关关係推求：
利用B定义域为7≤B≤9的整数的快捷方式：
1、当B=7时，整理式14有：50×（a+49）≤2979+49E≤55×（a+49）
因a定义域为1≤a≤6的整数,则
2500≤2979+49E≤3025，E≤0.94，故B＝7导致无意义，非正解。
2、当B=9时，根据式12有： （7+7a/49）×（9+C/7）＝60+E+273/343
即： 63+C+7a×（63+C）/343 ＝60+E+273/343
或： 7a×（63+C）＝343×（E-C-3）+273
这同样类似一个一次同余式：
7a×（63+C）≡273（mod 343）
在a和 C定义域为1≤且≤6的整数时，该式无正整数解。
3、当B=8时，根据式12有： （7+7a/49）×（8+C/7）＝60+E+273/343
或： 7a×（56+C）＝343×（E-C+4）+273
即一次同余式：
7a×（56+C）≡273（mod 343）
该同余式有一组解：a＝3，C＝6；则A＝7a＝21.
代入式12，有（7+3/7）×（8+ 6/7）＝60+ E +273/343，得：
E＝5
因此，上述所设五数分别为：A＝21，B＝8，C＝6，D＝7，E＝5.
从小广和大广的文意可知,该部分算数是已知田块的长和宽求面积,或已知面积、长或宽其中两项,求其第三项。本段“大广”是当长和宽都是带分数的情况下求其田亩面积。经过推理计算，可得知，该文所举例的长（广）为7又49分之21步，宽（纵）为8又7分之6步，面积为65又343分之273步。
结论：根据上下文意和推导，该段文字应为：
大广 广七步
《张家山汉简〈算数书〉》“大广”脱字补九分步之廿一，求纵八步七分步之六其田。为亩六十五步有（又）三百
《张家山汉简〈算数书〉》“大广”脱字补三分步之二百七十三。大广术（术）曰：直（置）广纵（纵）而各以其分母乘其上全步，令分子从之，令相乘也，为实，有（又）各令分母相乘，为法，如法得一步，不盈步以法命之。
参考文献：
李继闵：《演算法的源流（东方古典数学的特徵）》，科学出版社2006年。
《九章算术·方田》（国学网）
《孙子算经》（国学网）
（编者按：[1]张家山二四七号汉墓竹简整理小组：《张家山汉墓竹简[二四七号墓]》，2001年文物出版社，第98页。
[2]张家山二四七号汉墓竹简整理小组：《〈张家山汉墓竹简[二四七号墓] 〉释文修订本》，文物出版社2006年，第156页。
[3]《张家山汉墓竹简[二四七号墓]》第98页。 (责任编辑：admin)

原文出处：http://his.newdu.com/a/201711/05/514181.html

以上是关于《张家山汉简〈算数书〉》“大广”脱字补的介绍，希望对想了解历史故事的朋友们有所帮助。